YETI DOCS

RNN

송성근
2023년 12월 11일
언어 모델은 다음 단어가 무엇이 오는지 예측하는 작업이에요. 구체적으로 말하자면 연속적인 단어 x(1),x(2),⋯ ,x(t)x^{(1)}, x^{(2)}, \cdots, x^{(t)}가 주어질 때, 다음 단어 x(t+1)x^{(t+1)}의 확률을 예측하는 것이죠.
P(x(t+1)∣x(t),⋯ ,x(1))P(x^{(t+1)}|x^{(t)}, \cdots, x^{(1)})
이러한 시스템을 language model이라고 해요. 조금 더 생각해보면 언어 모델은 [EOS]이 나올 때 까지 문장의 모든 부분을 확률로 할당하는 시스템인 셈이죠.
P(x(1),⋯ ,x(T))=P(x(1))×P(x(2)∣x(1))×⋯×P(x(T)∣x(T−1),⋯ ,x(1))P(x^{(1)}, \cdots, x^{(T)}) = P(x^{(1)}) \times P(x^{(2)}|x^{(1)}) \times \cdots \times P(x^{(T)}|x^{(T-1)}, \cdots, x^{(1)})

N-Gram Language Model

N-Gram Language Models은 딥 러닝 이전 고전적인 언어 모델을 구현하는 방법입니다. n-gram은 연속된 단어 덩어리에요. 아래 예시를 보면 이해가 쉬울 것입니다.
1
Markov assumption은 이러한 덩어리를 이용하여 다음 단어가 무엇이 나올지 예측하는 방식입니다. 하나의 큰 corpus에서 나올 확률을 세는 방식이죠. 아래 4-gram 언어 모델의 예시를 보겠습니다.
P(w∣students  opened  their)=count(students  opened  their  w)count(students  opened  their)P(w | students \; opened \; their) = \frac{count(students \; opened \; their \; w)}{count(students \; opened \; their)}
여기서 "student opened thier"이 총 1000번 등장한다고 합시다.
"student opened their books"가 400번 등장하면 P(books∣student  opened  their)=0.4P(books | student \; opened \; their) = 0.4.
"student opened their exams"가 100번 등장하면 P(exams∣student  opened  their)=0.1P(exams | student \; opened \; their) = 0.1.
이런 식으로 계산이 되는 것이죠.
하지만 여기에는 몇 가지 문제가 있습니다.
Sparsity problem
  • "students opened their w" 라는 문장이 전혀 등장하지 않는다면 w에 대한 확률은 0이 됩니다.
    이럴 때에는 모든 w∈Vw \in V에 대해 카운트를 하여 적용하는 방법이 있을거에요. smoothing
  • "students opened their" 라는 문장이 전혀 등장하지 않는다면 "opened theire"로 대체하는 방법이 있을 거에요. 여기서 n이 클수록 이 문제가 자주 발생할 확률이 높겠죠.
Storage problem
  • 사용할 모든 n-gram의 수를 저장해야 하는 문제가 있죠. 이는 n이 커지고, corpus가 클수록 모델 사이즈가 커진다는 것이죠.
n-gram을 이용하여 아래와 같은 방식으로 문장을 생성할 수 있어요.
00 01
놀랍게도 문법적으로는 틀리지 않지만, 문맥에 맞지 않는 내용이 만들어지죠. 자연스럽게 문맥을 생성하려면 n을 키워야하고, 이는 모델 사이즈가 커지고 sparsity problem이 커지는 문제가 발생하죠.

RNN

위 문제를 해결하기 위해서 언어 모델에 인공 신경망을 사용하는 방법이 등장했어요.
02
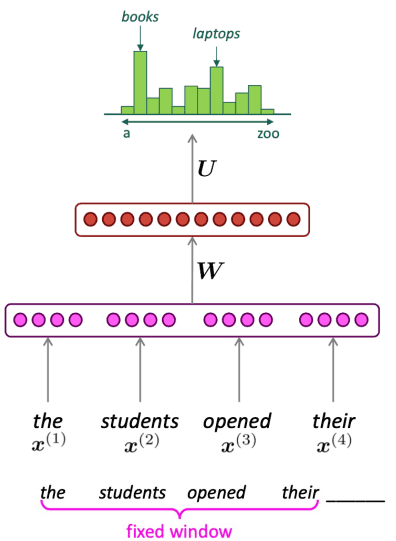
Sparsity problem을 해결하고 모든 n-gram을 저장할 필요가 없어졌어요. 하지만 window를 키우기 위해서는 WW도 커져야 하기에 window를 충분히 크게 만들 수 없습니다. 그래서 어떤 길이의 입력이든 처리할 수 있는 방법이 필요합니다.
03
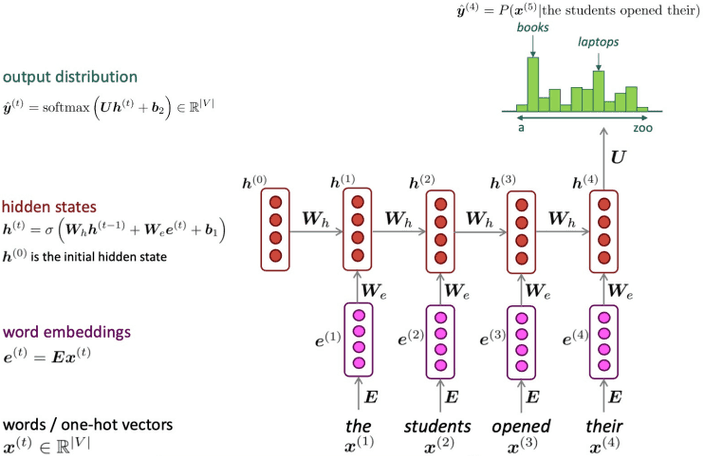
RNN의 기본 아이디어는 입력에 대해 동일한 WW를 사용하는 것이에요. RNN은 아래와 같은 특징을 가집니다.
  • 입력에 길이에 상관없이 처리할 수 있어요.
  • 이론적으로 tt 시점에서 정보는 이전 시점에서 모든 정보를 가지고 있어요.
  • 긴 입력이 들어와도 모델 사이즈는 커지지 않아요.
  • 연산 속도가 느립니다.
  • 실제로 오래 전 시점의 정보에 접근하긴 어렵습니다.

Training RNN

04
∂J∂W=1T∑t=1TJ(t)(θ)(1)\frac{\partial J}{\partial W} = \frac{1}{T} \sum_{t=1}^{T} J^{(t)} (\theta) \tag{1}
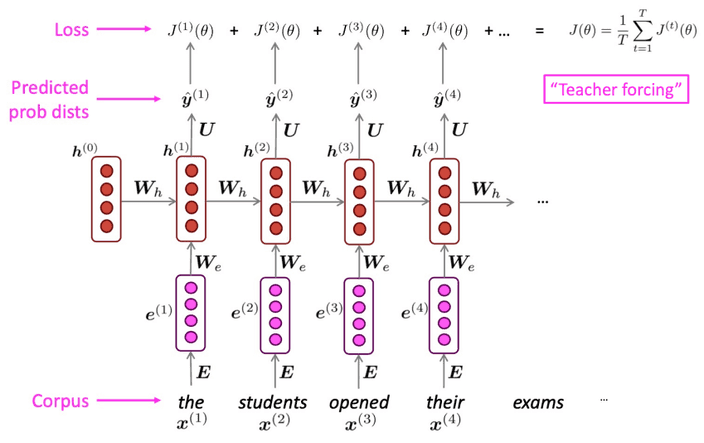
RNN을 학습하기 위해서 모든 결과에 대해 loss를 계산하고 이를 평균내 전체 loss를 구합니다. 하지만 실제로 우리가 다루는 입력은 문장이거나 어쩌면 문서가 될 수 있어요. 이런 방식으로 전체 corpus의 loss를 구하는 작업은 큰 연산을 필요로 하게 되죠. 이를 SGD와 같은 방식으로 어느정도 해결을 할 수 있겠죠.
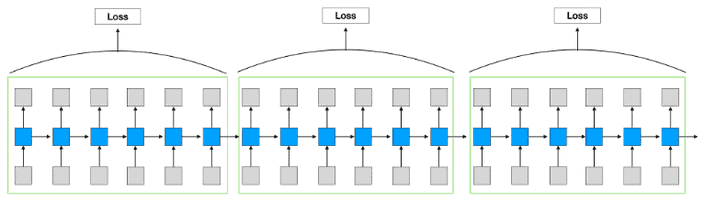10 혹은 전체 loss에 대해 계산하지 않고, 일부 길이마다 잘라 계산하는 형식으로 연산량을 줄일 수 있을거에요.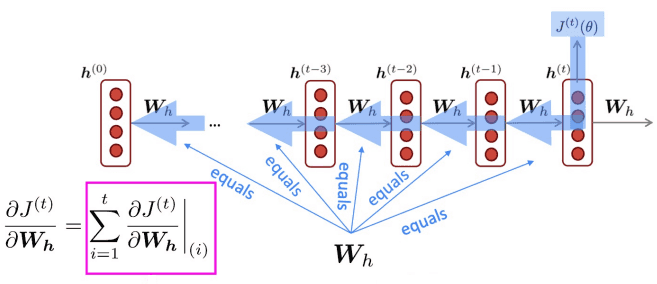
05
각 step마다 loss를 구하는 식은 아래와 같습니다.
h(t)=σ(Wxx(t)+Whh(t−1))(2)h^{(t)} = \sigma (W_x x^{(t)} + W_h h^{(t-1)}) \tag{2}
∂J(4)∂W=∂J(4)∂y^(t)∂y^(t)∂h(t)∂h(t)∂h(t−1)⋯∂h(1)∂W(3)\frac{\partial J^{(4)}}{\partial W} = \frac{\partial J^{(4)}}{\partial \hat{y}^{(t)}} \frac{\partial \hat{y}^{(t)}}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial h^{(t-1)}} \cdots \frac{\partial h^{(1)}}{\partial W} \tag{3}

Generate & Evaluate

RNN을 이용하여 텍스트를 생성하는 과정은 다음과 같아요.
06
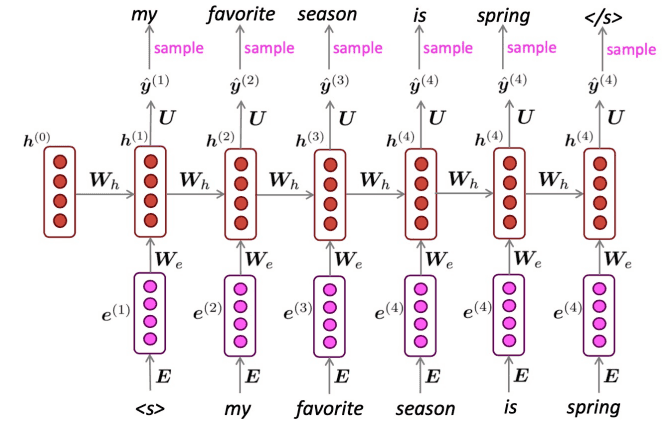
hidden state를 통해 예측한 단어를 다음 시점의 입력으로 사용하는 것이죠. 이렇게 [EOS]라는 단어가 나올 때 까지 반복하여 문장을 생성하는 것입니다. 이때 생성된 확률 분포에서 무작위로 단어를 선택하여 예측하는 repeated sampling을 사용합니다. 이는 확률이 높은 단어가 자주 선택되겠지만, 낮은 확률을 가진 출력도 선택될 수 있어요.
perplexity=∏t=1T(1PLM(x(t+1)∣x(t),⋯ ,x(1)))1/Tperplexity = \prod_{t=1}^{T} (\frac{1}{P_{LM} (x^(t+1) | x^(t), \cdots, x^(1))}) ^ {1/T}
이제 우리는 언어 모델의 평가 지표로 perplexity를 사용할거예요. 언어 모델에서 이전 단어들이 주어졌을 때 다음 단어에 대한 확률의 역수를 모두 곱하여 1T\frac{1}{T}승으로 normalization 한 것이죠. 이는 cross-entrophy를 이용한 loss J(θ)J(\theta)의 exponential을 한 것과 같습니다.
∏t=1T(1PLM(x(t+1)∣x(t),⋯ ,x(1)))1/T=∏t=1T(1y^xt+1(t))1/T=exp⁡(1T∑t=1T−log⁡y^xt+1(t))=exp⁡(J(θ))\prod_{t=1}^{T} (\frac{1}{P_{LM} (x^(t+1) | x^(t), \cdots, x^(1))}) ^ {1/T} = \prod_{t=1}^{T}(\frac{1}{\hat{y}_{x_{t+1}}^{(t)}})^{1/T} = \exp (\frac{1}{T} \sum_{t=1}^{T} - \log \hat{y}_{x_{t+1}}^{(t)}) = \exp (J(\theta))
우리는 loss가 낮아지도록 모델을 학습시켜요. 즉 perplexity는 점수가 낮을수록 잘 학습된 모델이라고 할 수 있겠네요.
뭐 문장 생성작업 외에도 entity recognition, text classification 등의 작업을 수행할 수 있어요.
07 08

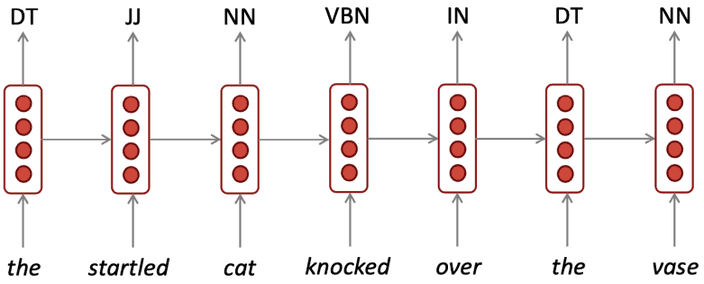
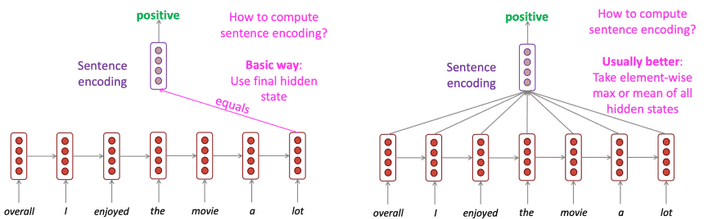
LSTM, RNN Variants

09
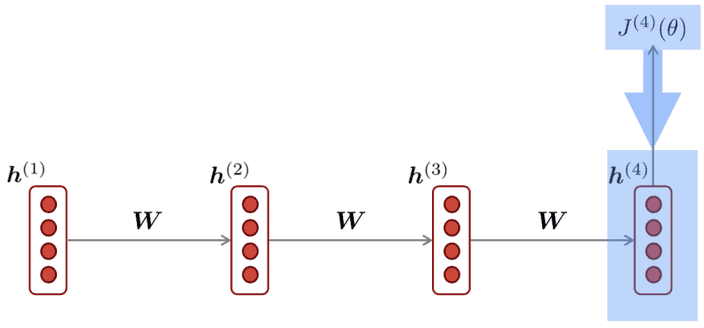
우리는 학습을 위해 식 (3)과 같이 loss에 대한 기울기를 계산하였습니다.
∂h(t)∂h(t−1)=∂h(2)∂h(1)×∂h(3)∂h(2)×⋯×∂h(t)∂h(t−1)(4)\frac{\partial h^{(t)}}{\partial h^{(t-1)}} = \frac{\partial h^{(2)}}{\partial h^{(1)}} \times \frac{\partial h^{(3)}}{\partial h^{(2)}} \times \cdots \times \frac{\partial h^{(t)}}{\partial h^{(t-1)}} \tag{4}
∂h(t)∂h(t−1)=Whh(t−1)(5)\frac{\partial h^{(t)}}{\partial h^{(t-1)}} = W_h h^{(t-1)} \tag{5}
식 (3)을 풀어보면 식 (4)의 형태가 등장하는데 식 (5)를 활용하면 WhW_h가 여러번 곱해지는 형태를 가지는 것을 볼 수 있어요. 만약 step tt가 크면 클수록 WhW_h가 더 많이 곱해지는 모습이 보이겠죠. 그런데 만약 ∣Wh∣>1\left| W_h \right| > 1 이라면 step이 길어질수록 loss에 대한 WhW_h의 기울기는 점점 더 커질거에요. 이 상태로 gradient descent를 한다면 minimum과 멀어지는 쪽으로 학습이 진행될 것입니다. 이를 exploding gradient라고 합니다. 이를 해결하기 위해서 기울기가 일정 크기 이상 커지면 적당한 값으로 clipping하는 방식으로 해결할 수 있을거예요.
반대로 ∣Wh∣<1\left| W_h \right| < 1 이라면 step이 길어질수록 loss에 대한 WhW_h의 기울기는 점점 더 작아질거에요. 이를 vanishing gradient라고 합니다. loss를 계산할 때 너무 먼 step과의 기울기를 구하는 것은 문제가 발생하게 됩니다.

LSTM

vanishing gradient 문제를 해결하기 위해 등장한 모델 구조가 LSTM (Long Short-Term Memory Network)입니다. LSTM은 기존 RNN에서 멀리 떨어진 정보에 대해 저장하는 cell이 추가된 형태에요. 이 cell로부터 정보를 읽고, 쓰고, 지우고를 할 수 있어요.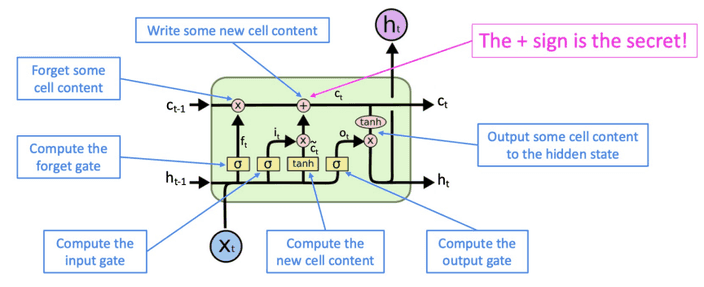
11
기능을 천천히 살펴봅시다.
12
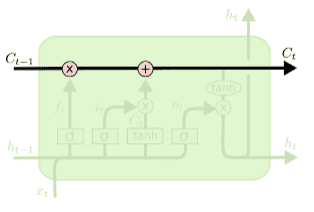
위 부분은 LSTM의 cell state 입니다. 이는 정보가 저장되는 장소에요.
13
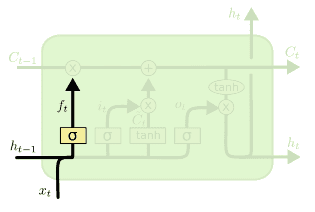
LSTM의 첫 단계는 cell state에 저장된 정보를 잊을지 보존할지 선택하는 경로에요. forget gate에서 ht−1h_{t-1}과 xtx_t를 WfW_f와 연산한 후 sigmoid를 통해 0과 1사이 값으로 만들어 줍니다. 만약 이 값이 1이 되면 모든 정보를 보존하고 0이되면 모든 정보를 버리는 것이 되겠죠. 실제로는 0~1 사이 값이 나올테니 일부 정보를 보존하고 버리는 식으로 진행되겠죠.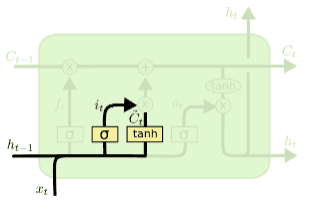
ft=σ(Wf⋅[ht−1,xt]+bf)f_t = \sigma (W_f \cdot [h_{t-1}, x_t] + b_f)
14
다음 단계는 앞으로 들어오는 정보 중 어떤 것을 cell에 저장할 지 정하는 부분이에요. input gate라고 불리는 sigmoid가 어떤 값을 업데이트할지 정합니다. 이를 tanh를 거친 정보와 곱해 cell에 전달합니다.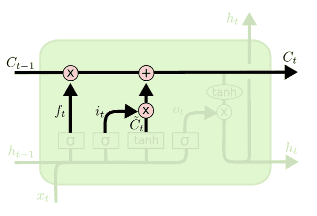
it=σ(Wi⋅[ht−1,xt]+bi)i_t = \sigma (W_i \cdot [h_{t-1}, x_t] + b_i)
C~t=tanh(WC⋅[ht−1,xt]+bC)\tilde{C}_t = tanh(W_C \cdot [h_{t-1}, x_t] + b_C)
15
forget gate와 input gate에서 생성된 정보를 이용하여 cell state를 업데이트 할거에요.
Ct=ft∗Ct−1+it∗C~tC_t = f_t * C_{t-1} + i_t * \tilde{C}_t
16
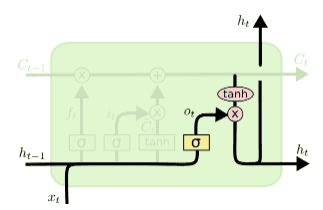
마지막으로 무엇을 output으로 보낼지 정하는 작업이 남아있어요. out gate에서 ht−1h_{t-1}과 xtx_t를 통해 어느 정보를 cell state에서 output으로 낼 것인지 결정합니다. cell state에 tanh를 거친 정보와 sigmoid와 곱해 결과를 만들어 내는 것이죠.
ot=σ(Wo[ht−1,xt]+bo)o_t = \sigma (W_o [h_{t-1}, x_t] + b_o)
ht=ot∗tanh(Ct)h_t = o_t * tanh(C_t)
이런 방식으로 우리는 오래된 정보를 기억하는 식으로 설계할 수 있습니다. 만약 forget gate가 1이고 input gate가 0이면 오래된 정보도 영원히 남아있을 수 있죠. 하지만 너무 깊은 neural network는 항상 optimization 문제가 발생했어요. 이를 residual connection을 통해 해결하고는 합니다.

Bidirectional and Multi-layer RNN

1
만약 우리는 위와 같이 문장의 빈칸에 어울릴 단어를 찾는 문제를 해결해야 한다면 어떻게 할까요? 먼저 문장의 끝까지 보고 빈칸에 'hungry'라는 단어가 들어갈 수 있다고 생각할 것입니다. 즉, 문장의 앞 뒤 정보를 아는 것은 단어를 선택하는 것에 있어 중요한 부분이라고 할 수 있죠. 하지만 기존 RNN은 예측하고자 하는 단어 뒤에 있는 정보를 알 수 없었어요. 이러한 문제를 해결하기 위해 Bidirectional RNN이 등장합니다.
1
위 예시를 볼게요. 우리는 이 문장의 감정을 분석하려고 합니다. 중간에 terribly라는 단어가 있지만 뒤에 있는 exciting을 보면 이 단어는 긍정적으로 사용되는 것을 알 수 있어요. 그래서 뒤에 있는 exciting의 정보를 앞으로 전달할 수 있는 모델을 설계할거에요. 방법은 간단해요 2개의 레이어를 사용하는 것입니다.
17
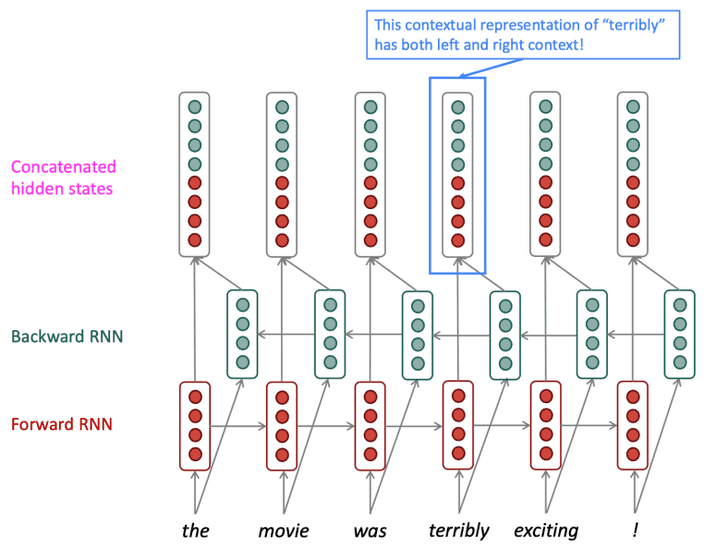
하나는 문장의 앞에서 뒤로 정보를 전달하는 레이어, 다른 하나는 뒤에서 앞으로 정보를 전달하는 레이어죠. 출력은 두 레이어의 정보를 합친 상태를 이용하여 output을 생산하는 방식이에요.
h→(t)=RNNFW(h→(t−1),x(t))\overrightarrow{h}^{(t)} = RNN_{FW}(\overrightarrow{h}^{(t-1)}, x^{(t)})
h←(t)=RNNFW(h←(t−1),x(t))\overleftarrow{h}^{(t)} = RNN_{FW}(\overleftarrow{h}^{(t-1)}, x^{(t)})
h(t)=[h→(t);h←(t)]h^{(t)} = [\overrightarrow{h}^{(t)}; \overleftarrow{h}^{(t)}]
RNN은 사실 여러 state를 거치기 때문에 그 자체로도 이미 깊다고 할 수 있어요. 이를 여러 레이어를 추가한 것이 multiple RNN입니다. 이는 더 복잡한 문제를 해결하는 데 사용할 수 있죠. 다른 말로는 stacked RNN이라고도 해요.